Indice degli argomenti
-
Introduzione ai Diagrammi di Bode
I diagrammi di Bode sono strumenti grafici fondamentali per l’analisi della risposta in frequenza dei circuiti e dei sistemi dinamici. Sono ampiamente utilizzati in elettronica, telecomunicazioni e automazione industriale per rappresentare come l’ampiezza e la fase di un segnale variano al variare della frequenza.
Questa rappresentazione consente di comprendere il comportamento di filtri, amplificatori, circuiti risonanti e sistemi di controllo, facilitando l’ottimizzazione delle prestazioni e la previsione delle risposte del sistema.
Struttura dei Diagrammi di Bode
I diagrammi di Bode sono composti da due grafici separati:
Diagramma del modulo (o guadagno), che rappresenta il rapporto tra il segnale di uscita e il segnale di ingresso in funzione della frequenza. L'asse verticale è espresso in decibel (dB), mentre l'asse orizzontale è in scala logaritmica.
Diagramma della fase, che mostra la variazione dell’angolo di fase tra ingresso e uscita in funzione della frequenza. Anche qui l’asse orizzontale è in scala logaritmica, mentre l’asse verticale è espresso in gradi (°).
Utilità e Applicazioni
I diagrammi di Bode sono strumenti essenziali per:
- Analizzare la risposta in frequenza di un sistema, identificando guadagni e sfasamenti.
- Progettare e ottimizzare filtri (passa-basso, passa-alto, passa-banda, notch).
- Studiare la stabilità dei sistemi di controllo, determinando margini di guadagno e di fase.
- Determinare la banda passante e la risposta dinamica di circuiti elettronici.
- Valutare il comportamento di circuiti RLC e amplificatori operazionali.
Rappresentazione Matematica e Funzione di Trasferimento (FDT)
Nei circuiti lineari, la risposta in frequenza è descritta dalla funzione di trasferimento (FDT):
Dove:
- |H(jω)| indica il modulo della funzione di trasferimento.
- φ(ω) rappresenta la fase.
Vantaggi dell’Uso della Scala Logaritmica
L’utilizzo della scala logaritmica nell’asse delle frequenze e del guadagno permette di:
- Rappresentare un ampio intervallo di frequenze in modo compatto.
- Visualizzare in modo chiaro le pendenze dei guadagni, espressi in dB/decade.
- Identificare facilmente punti chiave come frequenze di taglio, risonanza e margini di stabilità.
Conclusione
I diagrammi di Bode sono strumenti potenti per l’analisi dei circuiti e dei sistemi di controllo, fornendo una visione intuitiva della risposta in frequenza. La loro applicazione permette di progettare sistemi più efficienti, migliorando la stabilità e le prestazioni dei circuiti elettronici e industriali.
-
-
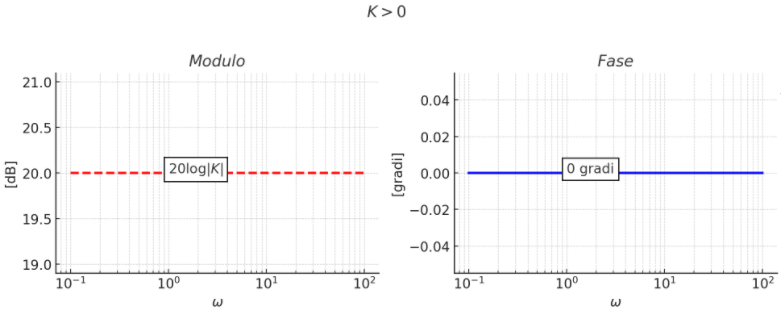
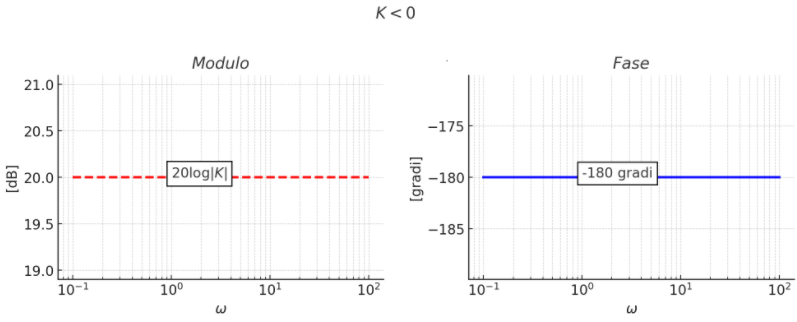
GUADAGNO COSTANTE G(s) = K
\( G(j \omega) = K \)
MODULO: \( |G(j \omega)_{dB} = 20 Log (K) \)
FASE:
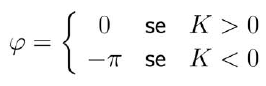
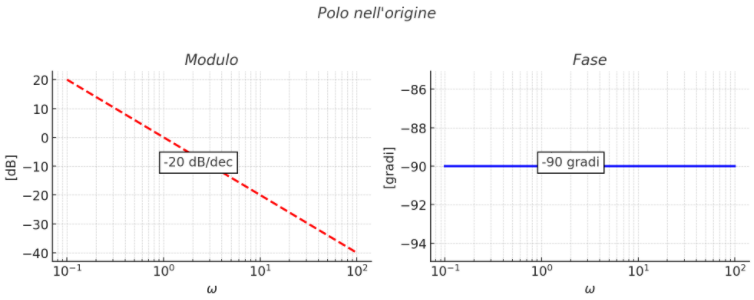
POLO NELL'ORIGINE G(s) = 1/s
\( G(j \omega) = \frac{1}{j \omega } \)
MODULO: \( |G(j \omega)_{dB} = 20 Log ( \frac{1}{ \omega}) \)
FASE:
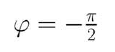
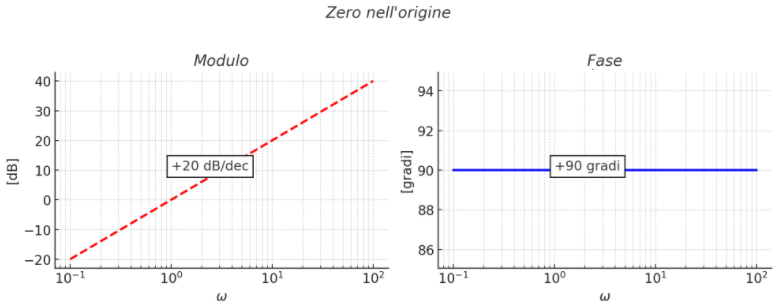
ZERO NELL'ORIGINE G(s) = s
\( G(j \omega) = {j \omega } \)
MODULO: \( |G(jω)|_{dB} = 20 Log (ω) \)
FASE:
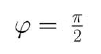
POLO REALE G(s) = 1/(s + ωn)
\( G(j \omega) = \frac{1}{1 + j \omega \tau } \)
MODULO: 0 per ω < ωn poi scende di 20 dB/dec
FASE:
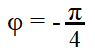per ω = ωn ; 0 una decade prima e -π/2 una decade dopo (polo reale negativo)FASE:
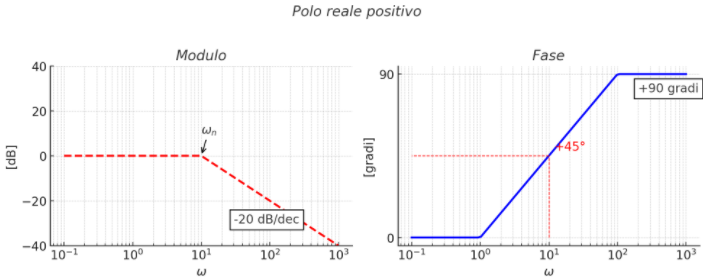
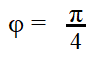per ω = ωn ; 0 una decade prima e π/2 una decade dopo (polo reale positivo)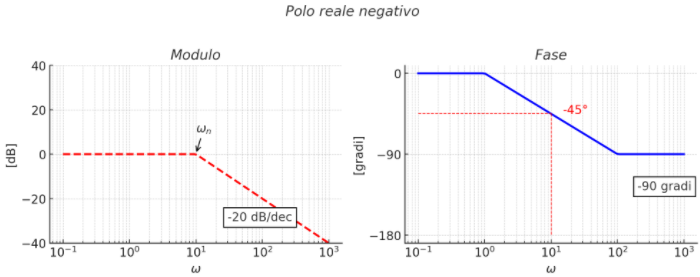
ZERO REALE G(s) = s + ωn
\( G(j \omega) = {1 + j \omega \tau } \)
MODULO: 0 per ω < ωn poi sale di 20 dB/dec
FASE:
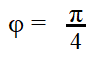per ω = ωn ; 0 una decade prima e π/2 una decade dopo (zero reale negativo)FASE:
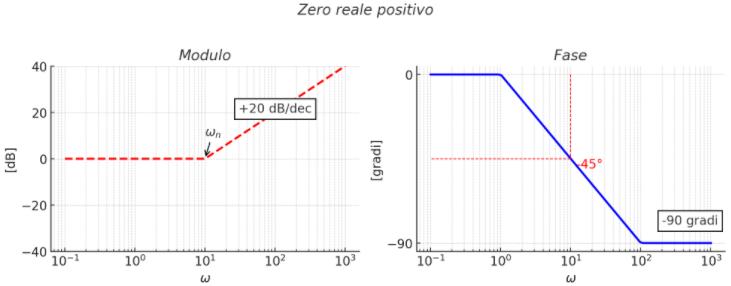
per ω = ωn ; 0 una decade prima e -π/2 una decade dopo (polo reale positivo)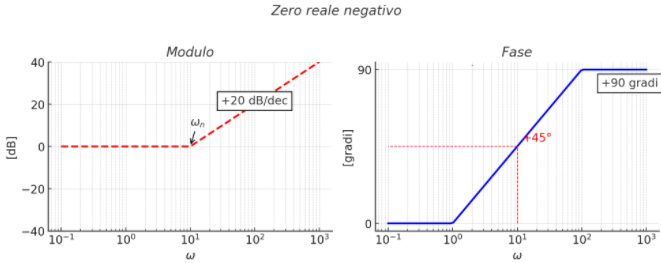
ZERI COMPLESSI CONIUGATI G(s) = s2 + 2ξωn s + ωn2
\( G(j \omega) = \omega^2_n [1 - \frac{ \omega^2}{\omega^2_n} + 2j \xi \frac{ \omega}{ \omega_n } ] \)
- se ξ > 1 si hanno due zeri reali e distinti, i cui valori sono \( z_{1,2} = - \omega_n ( \xi \pm \sqrt[]{ \xi^2 -1 } ) \);
- se ξ = 1 si hanno due zeri reali e coincidenti: z1,2 = − ωn;
- se ξ < 1 si hanno due zeri complessi coniugati.
Della formula sopra si ha che ωn2 viene incluso nella costante K, mentre si considerano modulo e argomento della parte reale e del coefficiente della parte immaginaria:
PARTE REALE = \( 1 - \frac{ \omega^2}{ \omega^2_n } \)
PARTE IMMAGINARIA = \( 2 \xi \frac{ \omega }{ \omega_n } \)
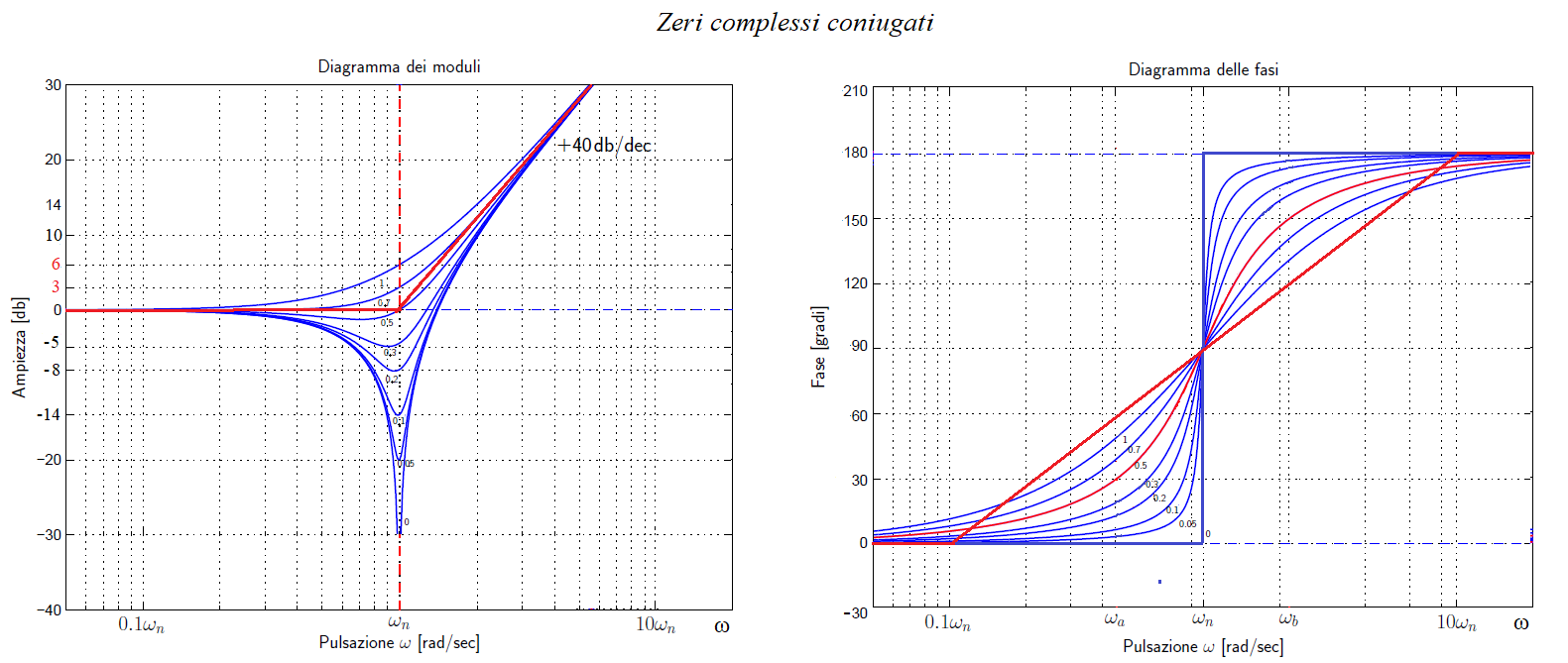
Si nota che il diagramma asintotico di Bode del modulo di una coppia di zeri complessi coniugati è costituito da una spezzata di due semirette, di cui una coincide con l’asse delle ascisse da ω = 0 ad ω = ωn; l’altra inizia da ω = ωn e sale con pendenza di 40 dB/decade, per ω → \( \infty \) .
Lo scostamento tra il diagramma reale e quello asintotico in questo caso non è fisso, come accade per gli zeri reali, ma dipende dal valore di ξ chiamato smorzamento. In particolare, il punto in cui la differenza tra la spezzata asintotica e la curva reale è massima si ha per ω = ωn.
La rappresentazione asintotica dell’argomento è costituita da una spezzata in tre parti:
- una semiretta coincidente con l’asse delle ascisse da ω = 0 ad ω = 0,1ωn;
- un segmento che si stacca dall’asse delle ascisse nel punto ω = 0,1ωn e sale con pendenza di 90° per decade, assumendo il valore ϕ = 90° per ω = ωn e terminando a ϕ = 180° per ω = 10ωn;
- una semiretta parallela all’asse delle ascisse in corrispondenza di ϕ = 180°, che inizia da ω = 10ωn e prosegue per ω → \( \infty \).
Anche il diagramma reale dell’argomento si discosta da quello asintotico di una quantità che dipende dal valore di ξ.
POLI COMPLESSI CONIUGATI G(s) = 1/(s2 + 2ξωn s + ωn2 )
\( G(j \omega) = \frac{1}{ \omega^2_n [1 - \frac{ \omega^2}{\omega^2_n} + 2j \xi \frac{ \omega}{ \omega_n } ]} \)
- se ξ > 1 si hanno due poli reali e distinti, i cui valori sono \( p_{1,2} = - \omega_n ( \xi \pm \sqrt[]{ \xi^2 -1 } ) \);
- se ξ = 1 si hanno due poli reali e coincidenti: p1,2 = − ωn;
- se ξ < 1 si hanno due poli complessi coniugati.
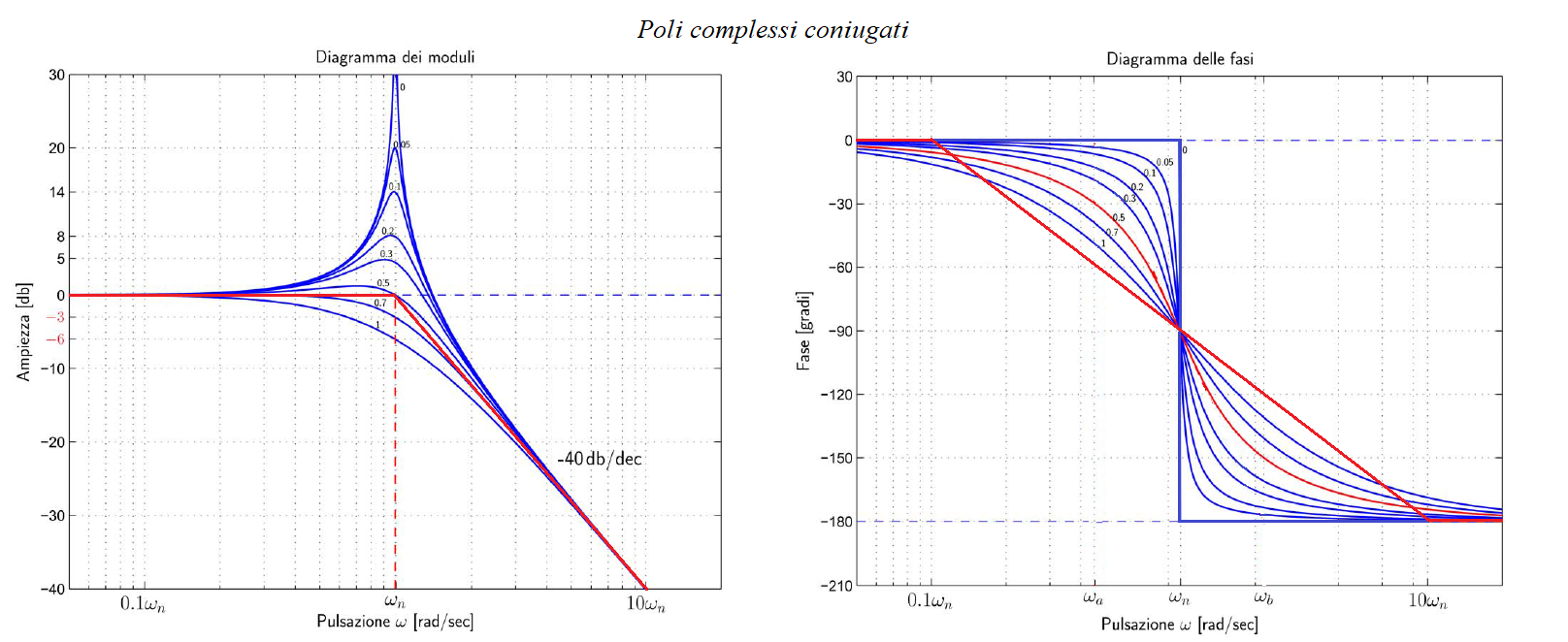
Le considerazioni sono analoghe a quelle degli zeri complessi coniugati.
Il diagramma asintotico di Bode del modulo di una coppia di poli complessi coniugati è costituito da una spezzata di due semirette, di cui una coincide con l’asse delle ascisse da ω = 0 ad ω = ωn; l’altra inizia da ω = ωn e scende con pendenza di 40 dB/decade, per ω → \( \infty \) .
Lo scostamento tra il diagramma reale e quello asintotico in questo caso non è fisso, come accade per i poli reali, ma dipende dal valore di ξ. In particolare, il punto in cui la differenza tra la spezzata asintotica e la curva reale è massima si ha per ω = ωn.
La rappresentazione asintotica dell’argomento è costituita da una spezzata in tre parti:
- una semiretta coincidente con l’asse delle ascisse da ω = 0 ad ω = 0,1ωn;
- un segmento che si stacca dall’asse delle ascisse nel punto ω = 0,1ωn e scende con pendenza di 90° per decade, assumendo il valore ϕ = - 90° per ω = ωn e terminando a ϕ = - 180° per ω = 10ωn;
- una semiretta parallela all’asse delle ascisse in corrispondenza di ϕ = - 180°, che inizia da ω = 10ωn e prosegue per ω → \( \infty \).
Anche il diagramma reale dell’argomento si discosta da quello asintotico di una quantità che dipende dal valore di ξ.
-
-