Topic outline
-
Introduzione alla Corrente Alternata (AC)
La corrente alternata (AC) è una forma di energia elettrica in cui la direzione e l’intensità della corrente variano periodicamente nel tempo. A differenza della corrente continua (DC), in cui il flusso di elettroni si muove in un’unica direzione, la corrente alternata cambia polarità a intervalli regolari, solitamente seguendo un’onda sinusoidale.
Nei sistemi di distribuzione elettrica, la corrente alternata è lo standard per il trasporto e la fornitura di energia elettrica, grazie ai seguenti vantaggi:
- Trasformabilità: la tensione può essere facilmente aumentata o ridotta tramite trasformatori, permettendo un trasporto efficiente su lunghe distanze con minime perdite.
- Maggiore efficienza nella trasmissione rispetto alla corrente continua, riducendo il riscaldamento dei conduttori.
- Compatibilità con motori elettrici e dispositivi industriali, che spesso operano con alimentazione AC.
- Frequenza (Hz): indica il numero di cicli completi al secondo (es. 50 Hz in Europa, 60 Hz negli Stati Uniti).
- Ampiezza e valore efficace: la tensione e la corrente variano nel tempo; il valore efficace (RMS) rappresenta l’equivalente in DC in termini di potenza dissipata.
- Fase e sfasamento: nei circuiti AC, tensione e corrente possono essere sfasate a causa della presenza di componenti reattivi come induttori e condensatori.
Rappresentazione Complessa e Fasoriale
Per semplificare l’analisi dei circuiti in corrente alternata, si utilizza la rappresentazione fasoriale, che sfrutta i numeri complessi per descrivere ampiezza e fase delle grandezze sinusoidali. In questa rappresentazione:
- Le tensioni e le correnti sono espresse come fasori, vettori rotanti nel piano complesso.Si facilita il calcolo di somma e differenza di segnali sinusoidali con lo stesso periodo.
- L’uso dell’esponenziale complesso consente di esprimere le relazioni tra grandezze in modo più compatto.
Impedenze e Circuiti RLC
Nei circuiti in corrente alternata, oltre alla resistenza (Ω), sono presenti componenti reattivi come:
Induttori (L), che oppongono una reattanza induttiva XL = ωL.
Condensatori (C), che oppongono una reattanza capacitiva XC = 1/(ωC).
L’impedenza è una grandezza complessa che generalizza la resistenza per includere gli effetti di induttori e condensatori:
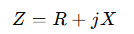
Dove:
- R è la parte reale (resistenza ohmica),
- X è la parte immaginaria (reattanza induttiva o capacitiva).
Risonanza nei Circuiti AC
Un aspetto fondamentale nei circuiti in corrente alternata è la risonanza, fenomeno che si verifica nei circuiti RLC serie o parallelo quando la reattanza induttiva e capacitiva si annullano tra loro:
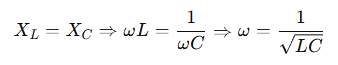
Alla frequenza di risonanza, il circuito presenta:
- Massimo trasferimento di potenza.
- Minima impedenza (nel caso serie) o massima impedenza (nel caso parallelo).
- Correnti elevate che possono causare sovraccarichi se non adeguatamente gestite.
Rifasamento nei Sistemi AC
Nei circuiti industriali, la presenza di carichi induttivi (motori, trasformatori) introduce sfasamento tra tensione e corrente, riducendo il fattore di potenza (cosφ) e aumentando le perdite di energia. Per migliorare l’efficienza della rete si utilizza il rifasamento, che consiste nell’aggiunta di condensatori per compensare la potenza reattiva e riportare il cosφ a valori più vicini a 1.
Il dimensionamento del rifasamento si basa sulla formula:
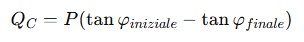
Dove QC è la potenza reattiva da compensare e P la potenza attiva.
Conclusione
La corrente alternata è il fondamento della distribuzione elettrica e dell’alimentazione industriale. La sua analisi richiede strumenti matematici come la rappresentazione fasoriale e il concetto di impedenza, mentre fenomeni come la risonanza e il rifasamento giocano un ruolo cruciale nel miglioramento dell’efficienza e nella gestione della potenza nei sistemi elettrici.
-
Un segnale sinusoidale è esprimibile con la funzione:
\( v(t) = V_{max} \cdot sen ( \omega t + \phi ) \)
in cui:
- Vmax è il valore di picco del segnale
- ω è la pulsazione in rad/s
- φ è la fase iniziale
Vediamo alcuni esempi con stessa frequenza (isofrequenziali) ma fase iniziale diversa:
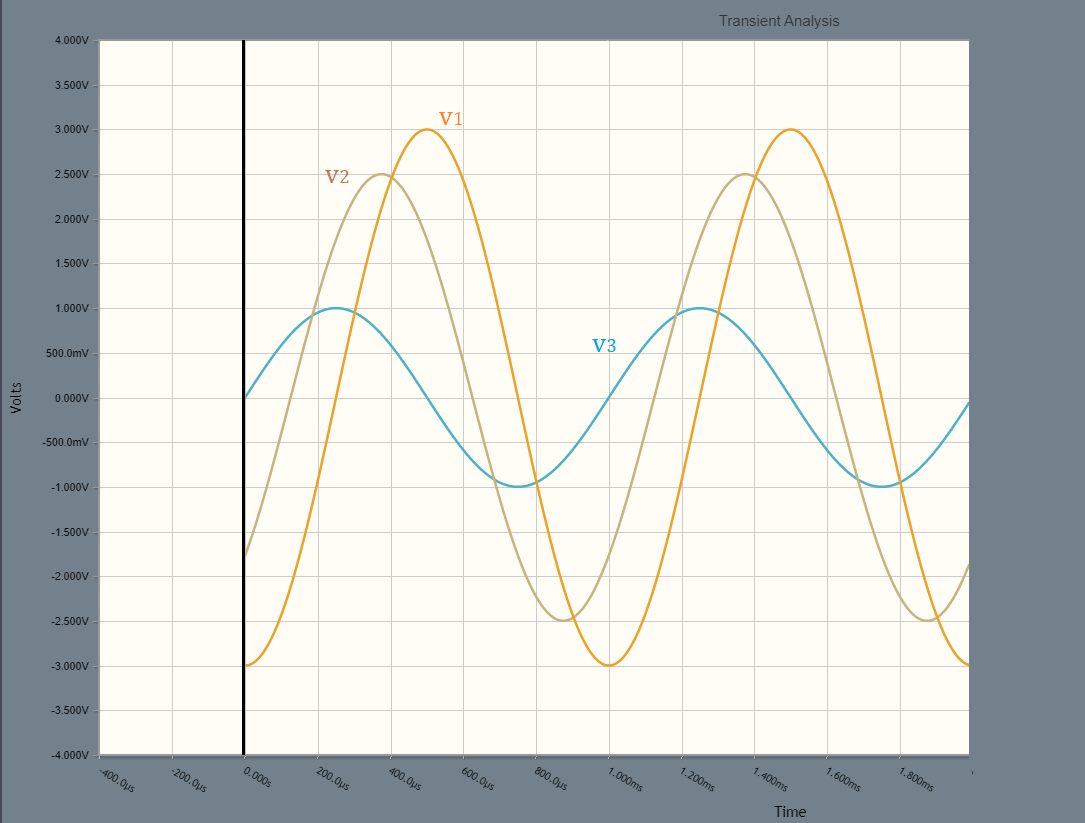
\( v_1 (t) = 3 \cdot sen (6283t + \frac{ \pi }{2} ) \) [φ = 90°]
\( v_2 (t) = 2,5 \cdot sen (6283t + \frac{ \pi}{6}) \) [φ = 30°]
\( v_2 (t) = 1 \cdot sen (6283t ) \) [φ = 0°]
E' possibile (ed estremamente utile) associare a segnali sinusoidali isofrequenziali dei vettori rotanti (detti FASORI) a velocità angolare pari alla pulsazione ω che sarà comune a tutti i segnali. Le proiezioni dei fasori sull'asse cartesiano saranno in funzione del tempo le sinusoidi dei segnali originali. -
Si definisce IMPEDENZA DI UN BIPOLO il rapporto complesso ottenuto da tensione e corrente.
\( \vec{Z} = \frac{ \vec{V}}{ \vec{I} } \)
Utilizzando il metodo simbolico anche in alternata tensioni e correnti sono rappresentate da frecce come in continua.
L'impedenza è, quindi, un numero complesso avente modulo pari al rapporto dei moduli e argomento pari allo sfasamento tra tensione e corrente.

L'impedenza è composta da una parte reale (ohmica che rappresenta la resistenza R) e una parte immaginaria (che rappresenta la reattanza X).
\( \vec{Z} = R + jX \)
La reattanza può essere capacitiva XC oppure induttiva XL .
Per quanto riguarda le impedenze in serie o in parallelo, l'impedenza equivalente si calcola con le formule uguali ai resistori.
- IMPEDENZE IN SERIE
- IMPEDENZE IN PARALLELO
-
La risonanza di tipo elettrico è un fenomeno caratterizzato da un valore di pulsazione (o frequenza) che instaura un comportamento particolare in un circuito.
Risonanza serie
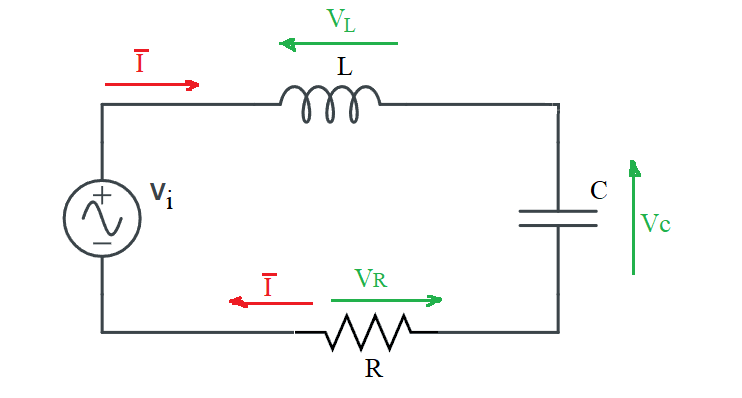
Dovendo calcolare l'impedenza equivalente avremo:
\( Z_{eq} = Z_R + Z_L + Z_C = R + jX_L - jX_C \)
Volendo calcolare modulo e fase:
\( | \vec{Z} | = \sqrt[]{R^2 + (X_L - X_C)^2} \)
\( \phi_z = arctan \frac{X_L - X_C}{R} \)
In corrispondenza di un valore di pulsazione ωr detto pulsazione di risonanza si ha la condizione di risonanza serie, valore per il quale :
\( X_L = X_C \)
la rete in questo caso si comporta come un circuito puramente resistivo, poiché il bipolo LC è come un cortocircuito e si ha, quindi, la corrente in fase con la tensione.
La formula si ricava in questo modo:
\( \omega_r \cdot L = \frac{1}{\omega_r \cdot C} \)
\( \omega_r = \sqrt[]{ \frac{1}{LC} } \)
La frequenza di risonanza sarà:
\( f_r = \frac{ \omega_r}{2 \pi } = \frac{1}{2 \pi \cdot \sqrt[]{LC} } \)
La rappresentazione vettoriale di tensione-corrente e dell'impedenza alla risonanza è la seguente:
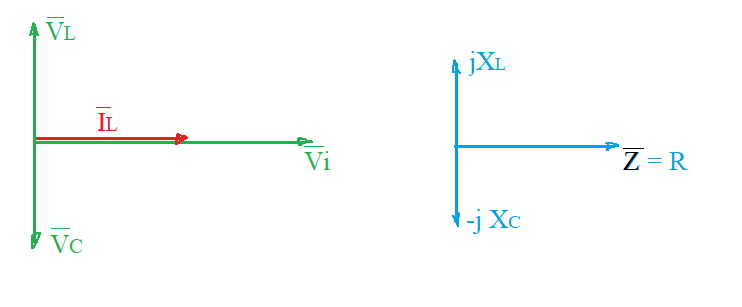
Risonanza parallelo
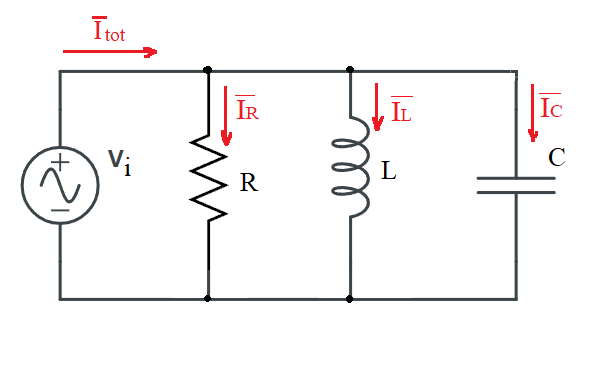
-
L'analisi delle reti lineari in regime sinusoidale permanente viene effettuato mediante il metodo simbolico; questo consiste nell'utilizzare la notazione fasoriale per semplificare i calcoli e descrivere le grandezze elettriche come grandezze vettoriali.
Questo è possibile poiché se la rete è lineare, qualunque grandezza al suo interno è di tipo sinusoidale e isofrequenziale rispetto al segnale di ingresso; in tal caso la frequenza può essere "messa da parte" e le grandezze rappresentate in forma complessa che contiene tutte le informazioni fondamentali (modulo e argomento) per ricostruire la forma sinusoidale.
Per approfondire vai alla sezione:
L'uso dei fasori e la loro forma complessa o polare permette di utilizzare TUTTE LE LEGGI E I PRINCIPI validi in continua: leggi di Ohm, Kirchhoff, Millman, Thevenin ecc con una notevole semplificazione delle relazioni integro-differenziali introdotte dai componenti reattivi.
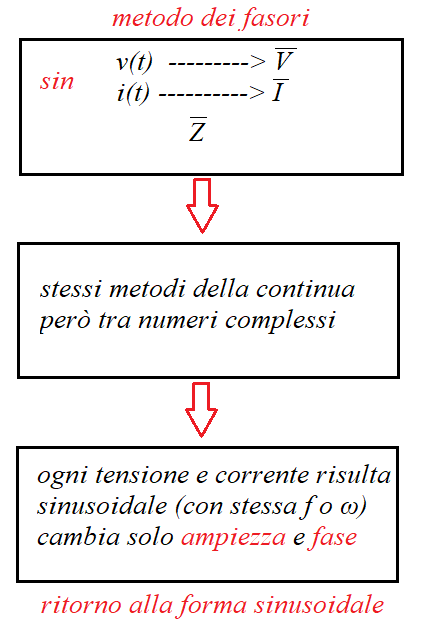
-
POTENZA IN ALTERNATA
In un circuito in corrente alternata (AC), esistono tre tipi di potenza: potenza attiva, potenza reattiva e potenza apparente.
La potenza attiva è la potenza effettivamente utilizzata dal circuito per eseguire un lavoro utile, come ad esempio alimentare un motore o una lampada. Essa è espressa in watt (W) ed è calcolata come il prodotto dei valori efficaci della tensione e della corrente, moltiplicato per il coseno dell'angolo di fase tra tensione e corrente.
\( P = V_{eff} \cdot I_ {eff} \cdot cos \phi \)
La potenza reattiva, invece, rappresenta la potenza scambiata tra il circuito elettrico e la rete elettrica, ma che non viene utilizzata per eseguire un lavoro utile. Essa è espressa in voltampere reattivi (VAR) ed è calcolata come il prodotto dei valori efficaci della tensione e della corrente, moltiplicato per il seno dell'angolo di fase tra tensione e corrente.
\( Q = V_{eff} \cdot I_ {eff} \cdot sen \phi \)
Infine, la potenza apparente rappresenta la potenza totale scambiata tra il circuito e la rete elettrica, sia la potenza utilizzata per eseguire un lavoro utile (potenza attiva) che quella scambiata ma non utilizzata (potenza reattiva). Essa è espressa in voltampere (VA) ed è calcolata come il prodotto dei valori efficaci della tensione e della corrente.
\( S = V_{eff} \cdot I_ {eff} \)
In sintesi, la potenza apparente è la somma vettoriale della potenza attiva e reattiva.
Le potenze si possono rappresentare tramite il TRIANGOLO DELLE POTENZE:
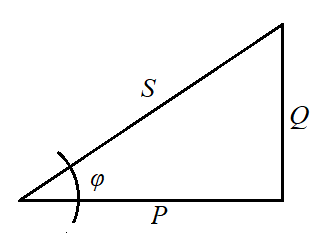
quindi si possono esprimere anche con:
- \( P = S \cdot cos \phi \)
- \( Q = S \cdot sen \phi \)
- \( \sqrt[]{P^2 + Q^2} \)
Inoltre se il bipolo è attraversato da una corrente di modulo \( I \):
- \( P = R \cdot I^2 \)
- \( Q = X \cdot I^2 \)
- \( S = |Z| \cdot I^2 \)
La potenza reattiva Q risulta positiva se è di tipo prevalentemente induttivo QL > 0, negativa se è di tipo prevalentemente capacitivo QC < 0.
-
Il rifasamento monofase si riferisce alla correzione del fattore di potenza in un circuito monofase, ovvero alla riduzione dell'angolo di sfasamento tra la tensione e la corrente elettrica in modo da aumentare l'efficienza energetica del circuito e ridurre i costi di energia elettrica.
Il fattore di potenza (cos φ) è un indicatore dell'efficienza con cui un circuito elettrico utilizza l'energia elettrica. Un fattore di potenza inferiore a 1 indica la presenza di una quantità significativa di potenza reattiva, che rappresenta l'energia scambiata tra il circuito elettrico e la rete elettrica, ma che non viene utilizzata per eseguire un lavoro utile.
Per correggere il fattore di potenza in un circuito monofase, si può utilizzare un condensatore in parallelo al carico (solitamente un motore o una pompa) per compensare la potenza reattiva induttiva generata dal carico stesso. In questo modo si riduce l'angolo di sfasamento tra la tensione e la corrente elettrica, migliorando il fattore di potenza del circuito.
In sintesi, il rifasamento monofase consiste nell'aggiunta di un condensatore in parallelo al carico per compensare la potenza reattiva induttiva del carico stesso, migliorando l'efficienza energetica del circuito e riducendo i costi di energia elettrica.
Per approfondire l'argomento vai a RIFASAMENTO -->
-
