Topic outline
-
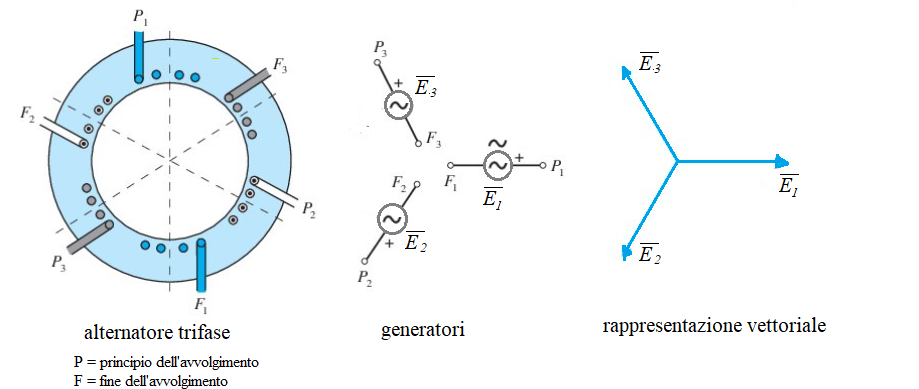
Un sistema trifase è costituito da 3 tensioni alternate sinusoidali isofrequenziali (cioè stessa frequenza che per l'Italia e l'Europa è 50 Hz) e viene generato dall'alternatore trifase che in un'unica macchina possiede tre avvolgimenti identici e sfasati di 120°.
Il sistema trifase è il modo più diffuso per produrre, distribuire a distanza e utilizzare energia elettrica in campo industriale.
Un sistema trifase si chiamerà simmetrico quando le tensioni oltre ad avere stessa frequenza sono uguali anche per valore efficace e sono sfasate di 120°.
Un sistema trifase si chiamerà equilibrato quando le correnti prodotte dalle tre corrispondenti tensioni, oltre ad avere stessa frequenza sono uguali anche per valore efficace e sono sfasate di 120°.
Il sistema trifase può essere schematizzato con 3 generatori di tensione \( \vec{E} \)1, \( \vec{E} \)2 , \( \vec{E} \)3 con modulo uguale e sfasati di 120°; ciascuno costituisce una fase : le 3 fasi vengono chiamate L1, L2, L3 oppure R, S, T.
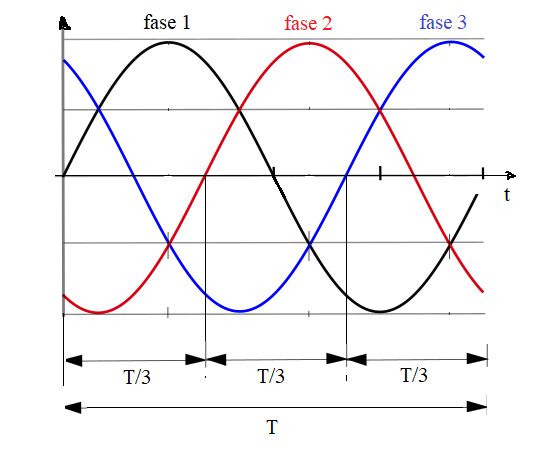
Forme d'onda del sistema trifase disponibili ai morsetti dell'alternatore.
Il primo vantaggio del sistema trifase è che richiede solamente quattro fili anziché sei necessari per tre sistemi monofase.
Infatti riunendo ciascun morsetto di fine avvolgimento ad un unico filo di ritorno chiamato neutro, si avrà una configurazione chiamata collegamento a stella con neutro.
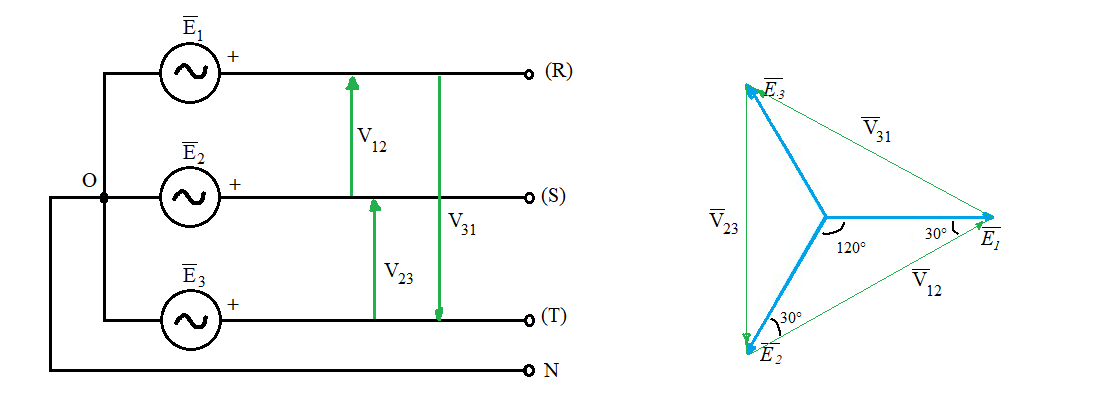
Esistono, quindi, due terne di tensioni:
- tensione tra le linee e il neutro \( \vec{E} \)1, \( \vec{E} \) 2 , \( \vec{E} \)3
- tensioni tra 2 linee \( \vec{V} \)12, \( \vec{V} \)23 , \( \vec{V} \)31
Le tensioni tra linea e neutro vengono chiamate tensioni stellate o di fase e sono indicate con E, mentre le tensioni tra linea e linea vengono chiamate tensioni concatenate o di linea e sono indicate con V.
La relazione tra tensioni di linea e tensioni di fase è la seguente:
\( \vec{E} \)1 (fase 0°) \( \vec{V} \)12 = \( \sqrt[]{3} \cdot \) \( \vec{E} \)1 (fase +30°)
\( \vec{E} \)2 (fase -120°) \( \vec{V} \)23 = \( \sqrt[]{3} \cdot \) \( \vec{E} \)2 (fase -90° o +270°)
\( \vec{E} \)3 (fase +120°) \( \vec{V} \)31 = \( \sqrt[]{3} \cdot \) \( \vec{E} \)3 (fase +150°)
Per quanto riguarda le correnti vengono chiamate correnti di linea quelle sulle tre linee (\( \vec{I} \)1, \( \vec{I} \)2, \( \vec{I} \)3 ), mentre per correnti di fase si intendono quelle che scorrono sulle impedenze di carico (\( \vec{I} \)f1, \( \vec{I} \)f2, \( \vec{I} \)f3 ).
-
Ad un generatore trifase possono essere collegate 3 impedenze Z1, Z2, Z3 in due modi:
- collegamento a stella: ciascuna impedenza è collegata tra una fase e il neutro, quindi ai suoi capi ha la tensione di fase Vf (E)
- collegamento a triangolo: ciascuna impedenza è collegata tra due fasi, quindi ai suoi capi ha la tensione di linea VL
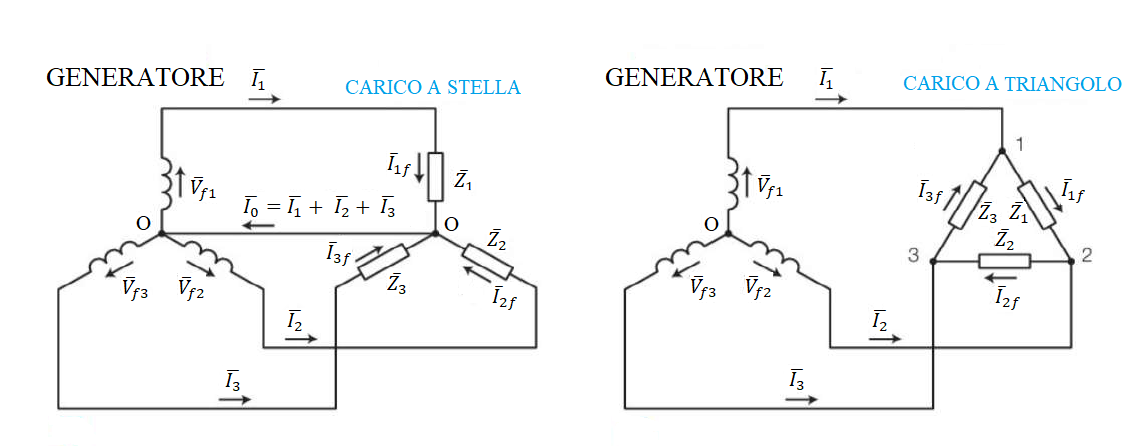
Il carico trifase è EQUILIBRATO se assorbe una terna simmetrica di correnti di linea (\( I_1, I_2, I_3 \) uguali in modulo e sfasate di 120°), cioè se tutte e 3 le impedenze di carico hanno stesso modulo e stesso argomento.
Le correnti che scorrono nelle impedenze di carico si chiamano correnti di fase (\( I_{1f}, I_{2f}, I_{3f} \)).
Carico equilibrato collegato a stella
- ai capi di ciascuna impedenza si ha la tensione di fase
- la corrente di fase nel carico è uguale a quella di linea
- la corrente sul neutro è nulla (è superfluo il cavo di neutro)
- il modulo delle correnti vale \( |I| = \frac{|V_f|}{|Z|} \)
- lo sfasamento tra tensioni e correnti φ è pari a quello dell'impedenza
Carico equilibrato collegato a triangolo
- ai capi di ciascuna impedenza si ha la tensione di linea
- le correnti di fase nel carico si calcolano con la legge di Ohm
\( \vec{I}_{1f} = \frac{ \vec{V}_{12}}{ \vec{Z}_1} \) \( \vec{I}_{2f} = \frac{ \vec{V}_{23}}{ \vec{Z}_2} \) \( \vec{I}_{3f} = \frac{ \vec{V}_{31}}{ \vec{Z}_3} \)
- le correnti di linea si calcolano applicando il 1° principio di Kirchhoff ai nodi 1, 2 e 3:
\( \vec{I} _1 = \vec{I}_{1f} - \vec{I}_{3f} \) \( \vec{I} _2 = \vec{I}_{2f} - \vec{I}_{1f} \) \( \vec{I} _3 = \vec{I}_{3f} - \vec{I}_{2f} \)
- la relazione che lega i moduli delle correnti è:
\( | \vec{I}| = \sqrt[]{3} \cdot | \vec{I}_f| \)
-
Per le potenze in trifase vale come quelle monofase in Teorema di Boucherot e cioè la potenza attiva P è la somma delle potenze attive assorbite dalle singole fasi.
(\( {P} \)tot = \({P} \)1 + \( {P} \)2 + \( {P} \)3 ... )
Analogamente la potenza reattiva Q sarà:
(\( {Q} \)tot = \({Q} \)1 + \( {Q} \)2 + \( {Q} \)3 ... )
e la potenza apparente S:
\( S = \sqrt[]{P^2 + Q^2} \)
POTENZE PER CARICHI EQUILIBRATI
Per carichi equilibrati la potenza attiva può essere espressa così:
\( P = 3 \cdot | \vec{V}\)f | \(\cdot | \vec{I}| \cdot cos \phi = \sqrt[]{3} \cdot | \vec{V}\)L| \(\cdot | \vec{I} | \cdot cos \phi \)
dove \( \vec{V}f \) è la tensione di fase (stellata) del generatore, \( \vec{I} \) è la corrente di linea e φ è il loro sfasamento.
\( Q = 3 \cdot | \vec{V}\)f | \(\cdot | \vec{I}| \cdot sen \phi = \sqrt[]{3} \cdot | \vec{V}\)L| \(\cdot | \vec{I} | \cdot sen \phi \)
e la potenza apparente S:\( S = 3 \cdot | \vec{V}\)f | \(\cdot | \vec{I}| = \sqrt[]{3} \cdot | \vec{V}\)L| \(\cdot | \vec{I} | \)
Inoltre le relazioni tra P, Q e S nonché il triangolo delle potenze è identico al caso monofase.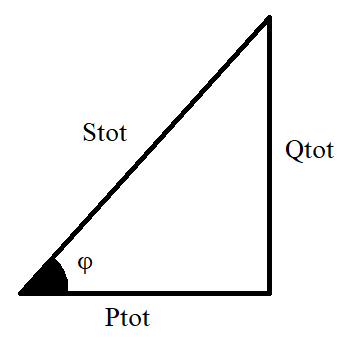
\( \phi = tan ^{-1 } ( \frac{Qtot}{Ptot} ) \)
-
Le trasformazioni stella-triangolo e triangolo-stella sono utili nel caso di più carichi trifase collegati per semplificare i calcoli.
Trasformazione stella - triangolo
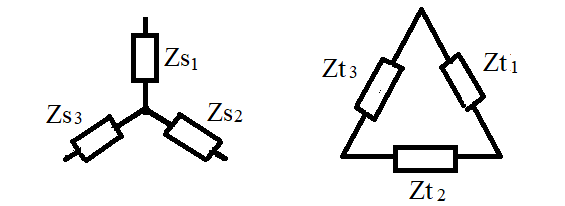
\( Z_{t1} = Z_{s1} \cdot Z_{s2} \cdot ( \frac{1}{Z_{s1}} + \frac{1}{Z_{s2}} + \frac{1}{Z_{s3}} ) \)
\( Z_{t2} = Z_{s2} \cdot Z_{s3} \cdot ( \frac{1}{Z_{s1}} + \frac{1}{Z_{s2}} + \frac{1}{Z_{s3}} ) \)
\( Z_{t3} = Z_{s3} \cdot Z_{s1} \cdot ( \frac{1}{Z_{s1}} + \frac{1}{Z_{s2}} + \frac{1}{Z_{s3}} ) \)
Se il CARICO è EQUILIBRATO \( Z_t = 3 \cdot Z_s \)Trasformazione triangolo - stella
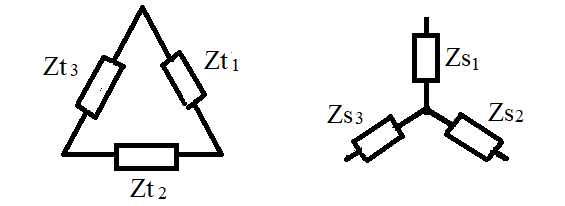
\( Z_{s1} = \frac{Z_{t1} \cdot Z_{t3} }{Z_{t1} + Z_{t2} + Z_{t3}} \)
\( Z_{s2} = \frac{Z_{t2} \cdot Z_{t1} }{Z_{t1} + Z_{t2} + Z_{t3}} \)
\( Z_{s3} = \frac{Z_{t3} \cdot Z_{t2} }{Z_{t1} + Z_{t2} + Z_{t3}} \)
Se il CARICO è EQUILIBRATO \( Z_s = \frac{Z_t}{3} \) -
-
La normativa
