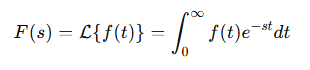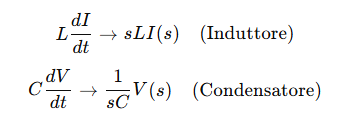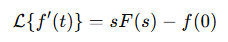Introduzione alla Trasformata di Laplace
La trasformata di Laplace è uno strumento matematico fondamentale in elettrotecnica, automazione e teoria dei circuiti, utilizzato per analizzare sistemi dinamici e risolvere equazioni differenziali in modo più semplice ed efficace.
Sfrutta la trasformazione da dominio del tempo (t) a dominio complesso (s), permettendo di rappresentare equazioni differenziali come equazioni algebriche, semplificando i calcoli nei circuiti elettrici e nei sistemi di controllo.
Definizione della Trasformata di Laplace
La trasformata di Laplace di una funzione t ≥ 0, è definita come:
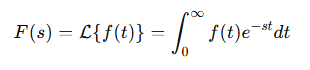
Dove:
- è la funzione nel dominio del tempo.
- è la sua rappresentazione nel dominio complesso di Laplace.
- è la variabile complessa (parte reale , parte immaginaria ).
📌 La trasformata permette di analizzare la risposta dei sistemi senza risolvere direttamente equazioni differenziali.
Perché si Usa la Trasformata di Laplace in Elettrotecnica?
✅ Semplificazione delle equazioni differenziali
- Le derivate diventano moltiplicazioni per s, trasformando le equazioni differenziali in equazioni algebriche.
✅ Analisi dei circuiti in modo più intuitivo
- Componente reattivi come induttori e condensatori si rappresentano con impedenze nel dominio di Laplace:
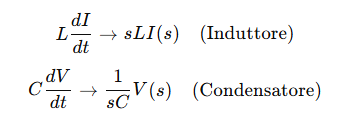
✅ Facilita lo studio della stabilità dei sistemi di controllo
- Determina la risposta ai transitori e le condizioni di stabilità di un circuito o di un sistema dinamico.
✅ Analisi dei sistemi lineari
- Utilizzata per lo studio di funzioni di trasferimento, rappresentando i sistemi con poli e zeri.
Proprietà Utili della Trasformata di Laplace
✔ Linearità → La trasformata di una somma è la somma delle trasformate.
✔ Derivazione → Una derivata diventa una moltiplicazione per s:
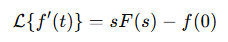
✔ Traslazione nel tempo → Utile per segnali ritardati.
✔ Teorema del Valore Iniziale e Finale → Permette di determinare i limiti della funzione nel tempo.
Applicazioni della Trasformata di Laplace
📌 Analisi di circuiti RLC → Studio delle risposte transitorie e stazionarie.
📌 Automazione e Controllo → Determinazione della stabilità e analisi di sistemi dinamici.
📌 Filtri e Segnali → Progettazione e analisi di filtri elettronici e sistemi di elaborazione del segnale.
📌 Elettronica di Potenza → Modellazione di convertitori e alimentatori switching.
La trasformata di Laplace è quindi uno strumento potente e versatile, che semplifica notevolmente l’analisi e la progettazione di sistemi elettrici e di controllo.