Indice degli argomenti
-
Alla base dell'algebra booleana c'è il concetto di variabile binaria, cioè una variabile che può assumere due soli valori.
Se si pensa allo stato di un interruttore che può essere acceso (ON) o spento (OFF) si ha un esempio di variabile binaria. Ad una variabile binaria si può associare anche una breve affermazione che può risultare vera o falsa.
Se una variabile digitale può assumere due soli livelli (alto H o basso L) è anch'essa una variabile binaria. Nell'algebra booleana i due valori sono associati ai simboli 0 e 1.
Anche nell'algebra booleana esiste il concetto di funzione. Una variabile Y detta variabile dipendente è funzione della variabile indipendente A quando il suo valore dipende da quello assunto da A.
Y = f(A)
Siccome A è binaria anche Y lo sarà. Viene chiamata tavola di verità la tabella che esprime la relazione tra variabile indipendente (variabile di ingresso) e la variabile dipendente (variabile di uscita).
Funzione NOT
La funzione NOT indica la negazione (o complemento o inverso) dell'ingresso.
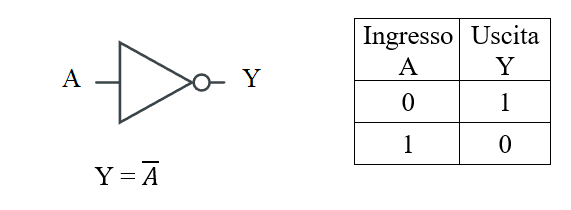
Si indica con un trattino sopra la variabile A.
Funzione AND
La funzione AND indica il prodotto logico. Può riguardare più variabili in ingresso. L'uscita assume valore 1 SE e SOLO SE TUTTE le variabili in ingresso sono uguali a 1.
Si indica con un puntino tra le variabili che spesso viene omesso per semplicità.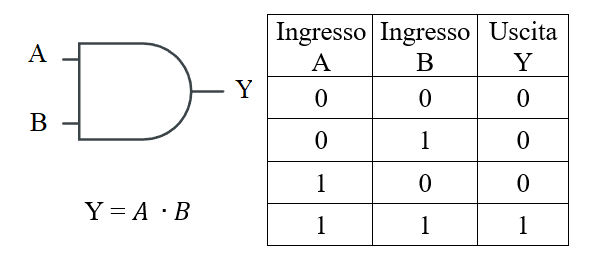
Proprietà commutativa.\( Y = AB = BA \)
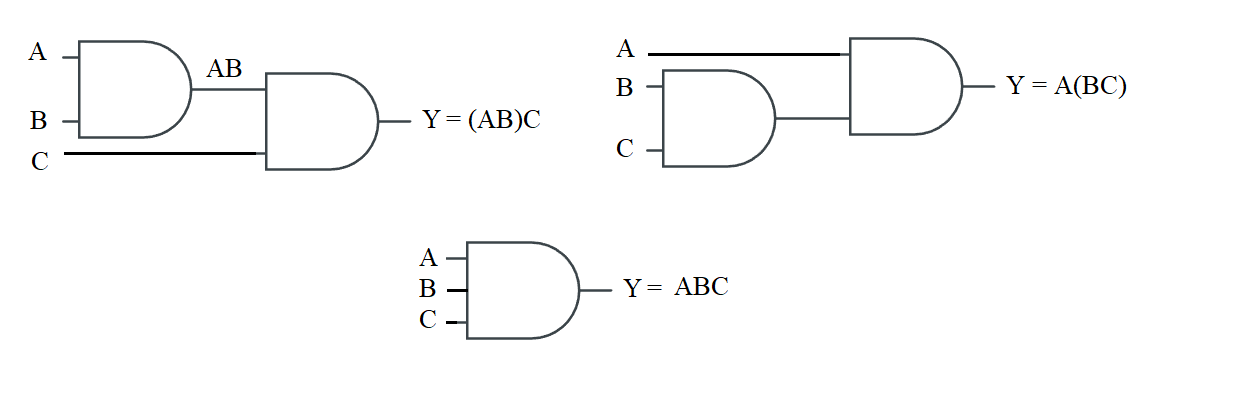
Proprietà associativa.
\( Y = (AB)C = A(BC) = ABC \)
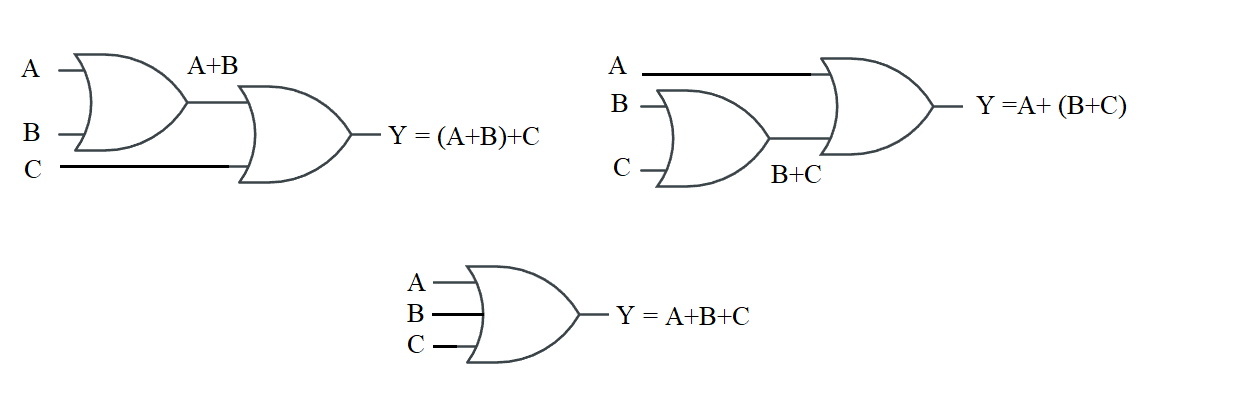
Funzione OR
La funzione AND indica la somma logica. Può riguardare più variabili in ingresso. L'uscita assume valore 1 SE ALMENO UNA delle variabili in ingresso è uguale a 1.
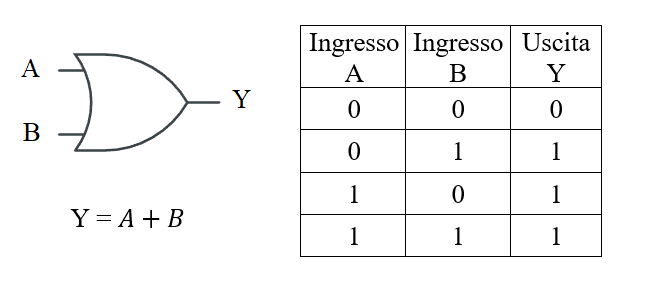
Si indica con un + tra le variabili.
Proprietà commutativa.\( Y = A+B = B+A \)
Proprietà associativa.
\( Y = (A+B)+C = A+(B+C) = A+B+C \)
Funzione NAND
Si ricava negando l'uscita di una funzione AND.
Si indica con un puntino tra le variabili (o senza nulla) e un tratto sopra.
Funzione NOR
Si ricava negando l'uscita di una funzione OR.
Si indica con un + tra le variabili e un tratto sopra.
Funzione EX-OR
La funzione OR ESCLUSIVO indica quando gli ingressi sono diversi. Può riguardare più variabili in ingresso. L'uscita assume valore 1 un numero dispari di ingressi è uguale a 1, mentre quando il numero degli 1 in ingresso è pari, l'uscita vale 0.
Si indica con il segno \( \oplus \) tra le variabili.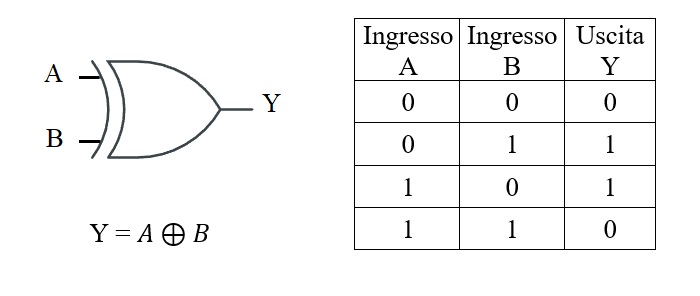
Funzione EX-NOR
La funzione NOR ESCLUSIVO si ottiene negando l'uscita di una EX-OR. Indica quando gli ingressi sono uguali. L'uscita assume valore 1 un numero spari di ingressi è uguale a 1, mentre quando il numero degli 1 in ingresso è dispari, l'uscita vale 0.
-
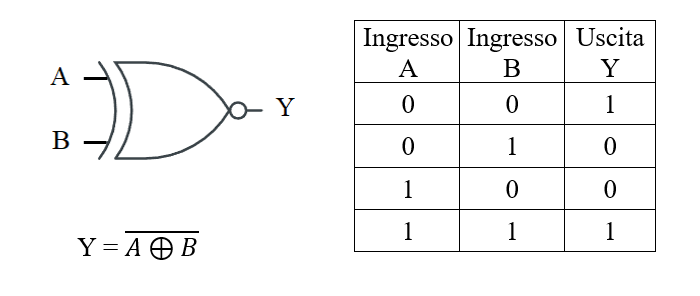
Viene applicata a tutte le forme di analisi di tipo logico.
Ogni volta che ad una frase è possibile associare un concetto che può essere solo vero o falso, l'algebra booleana può esprime il legame in forma concisa.
Esempi:
- Oggi piove (A) -----> NOT -----> oggi non piove (Ā)
- Se piove (A) o fa freddo (B) mi metto il cappotto (Y) ---> Y = A + B
- Se piove (A) e fa freddo (B) sto a casa (Y) ----> Y = AB
- Se il calzino destro (A) è diverso dal calzino sinistro (B) allora cambio i calzini (Y) ---> Y = A \( \oplus \)B
- Se il calzino destro (A) è uguale al calzino sinistro (B) allora mi metto le scarpe (Y) ---> \( \overline {A \oplus B} \)
Un'applicazione più inerente al campo elettrico è quella chiamata LOGICA DEI CONTATTI.
Ad una variabile di ingresso viene associato un contatto elettrico. Normalmente (in quella che è chiamata logica positiva) al valore logico 1 viene assegnato lo stato ON (contatto chiuso), mentre al valore logico 0 viene assegnato lo stato OFF (contatto aperto).
Alla variabile di uscita viene associato lo stato del carico: ad esempio una bobina (eccitata= 1, diseccitata=0) oppure una lampada (accesa = 1, spenta =0).
Queste convenzioni sono ampiamente utilizzate nei PLC.
Come vengono implementate elettricamente le funzioni logiche fondamentali?
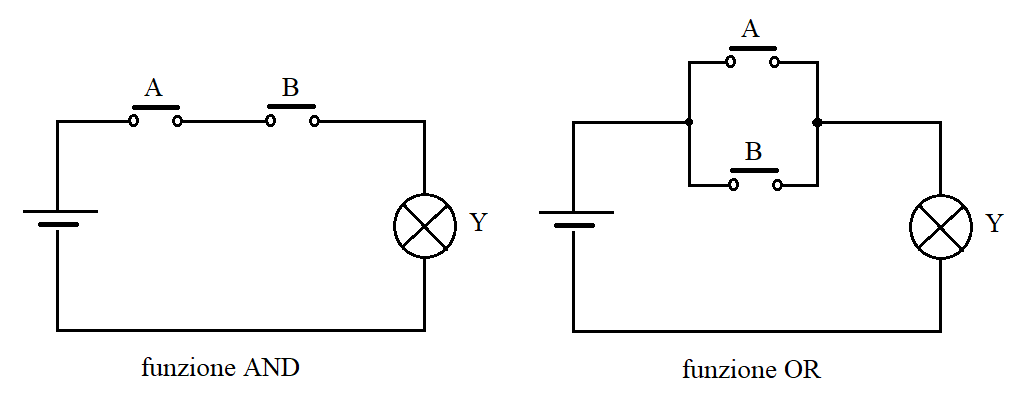
AND - Se i contatti sono posti in serie, la lampada è accesa solo se entrambi i contatti sono chiusi (ON)
OR - Se i contatti sono posti in parallelo, la lampada è accesa se almeno uno dei contatti è chiuso (ON)
Nei casi sopra i contatti sono normalmente aperti, cioè a riposo sono aperti. Esistono anche contatti normalmente chiusi (cioè a riposo sono chiusi), per poter implementare la negazione.
-
Le operazioni logiche fondamentali (NOT, OR, AND) permettono di esprimere qualsiasi funzione logica per quanto complessa sia.
Esistono proprietà e teoremi che consentono di semplificare le funzioni logiche.
-