Indice degli argomenti

  • Introduzione

    Minimizza tutto Espandi tutto

    Introduzione ai Numeri Complessi in Elettrotecnica: Perché si Usano?

    In elettrotecnica, i numeri complessi sono uno strumento fondamentale per l’analisi dei circuiti in corrente alternata (AC). Consentono di rappresentare in modo compatto e intuitivo grandezze sinusoidali, come tensione e corrente, semplificando i calcoli e la comprensione dei fenomeni elettrici.


    Perché si Usano i Numeri Complessi?

    L’uso dei numeri complessi in elettrotecnica nasce dall’esigenza di semplificare l’analisi dei circuiti in AC. Vediamo perché:

    ✅ Rappresentazione delle grandezze sinusoidali
    Un segnale sinusoidale può essere espresso nella forma generale:

    v(t)=Vmcos⁡(ωt+φ)v(t) = V_m \cos(\omega t + \varphi)

    Dove:

    • VmV_m è l’ampiezza della sinusoide.
    • ω\omega è la pulsazione (ω=2πf)
    • φ\varphi è la fase.

    Risolvere equazioni differenziali per questi segnali risulterebbe complesso. Per questo si utilizza la notazione fasoriale, che sfrutta i numeri complessi per trasformare le equazioni differenziali in equazioni algebriche.

    ✅ Notazione Fasoriale: Dalla Sinusoide al Numero Complesso
    Attraverso la rappresentazione in forma esponenziale di Eulero:

    ejθ=cos⁡θ+jsin⁡θe^{j\theta} = \cos\theta + j\sin\theta

    una sinusoide può essere scritta come un numero complesso (fasore):

    V=Vmejφ=Vm(cos⁡φ+jsin⁡φ)V = V_m e^{j\varphi} = V_m (\cos\varphi + j\sin\varphi)

    Questa notazione permette di:
    ✔ Semplificare i calcoli con tensioni e correnti alternate.
    ✔ Sommare e sottrarre sinusoidi con facilità.
    ✔ Sostituire derivate e integrali con moltiplicazioni e divisioni.


    Impedenza e Numeri Complessi

    Nei circuiti in AC, i componenti reattivi (induttori e condensatori) introducono uno sfasamento tra tensione e corrente. Grazie ai numeri complessi, possiamo definire l’impedenza (ZZ), che rappresenta l’opposizione al passaggio della corrente in regime sinusoidale:

    Questa rappresentazione permette di applicare le leggi di Ohm e Kirchhoff direttamente ai numeri complessi, semplificando l’analisi dei circuiti AC.

    Vantaggi dell'Uso dei Numeri Complessi in Elettrotecnica

    ✔ Semplificazione del calcolo dei circuiti AC
    ✔ Gestione intuitiva di grandezze con ampiezza e fase
    ✔ Facilità nel trattare componenti reattivi (L e C) come resistenze complesse
    ✔ Trasformazione di equazioni differenziali in equazioni algebriche

    Grazie ai numeri complessi e alla notazione fasoriale, i circuiti in corrente alternata possono essere analizzati con le stesse tecniche dei circuiti in corrente continua, rendendo l'elettrotecnica molto più intuitiva ed efficace.


  • Breve cenno alla trigonometria

    Definizioni delle funzioni trigonometriche

    Considerando il cerchio unitario sottostante, il raggio è il segmento OA = 1.

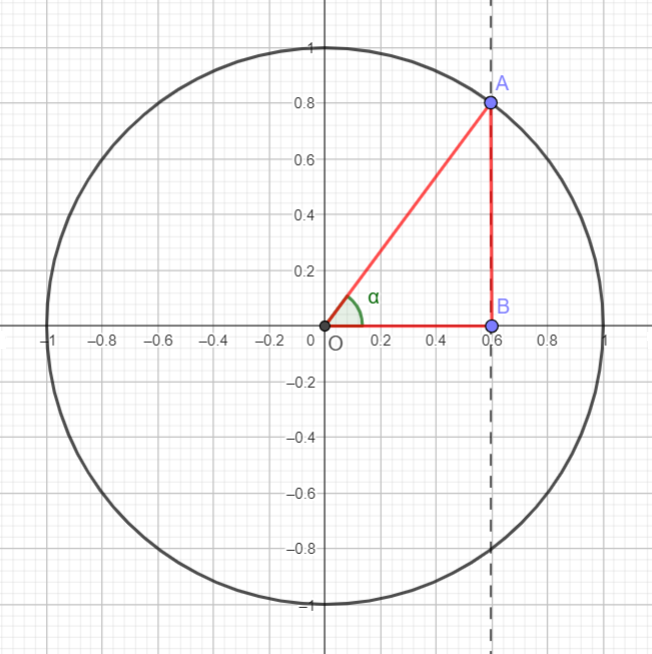
    trigonometria cerchio unitario 1

    Viene definito seno dell'angolo α ( e si indica sen α) il segmento AB, mentre coseno dell'angolo α ( e si indica cos α) il segmento OB.

    Il triangolo OBA è rettangolo e, pertanto, utilizzando il Teorema di Pitagora si ha:

    OB2  + AB2 = OA2  = 1

    Si ha la relazione trigonometrica 

    cos2 α + sen2 = 1

    Viene definito tangente dell'angolo α ( e si indica tan α) il rapporto tra seno e coseno di un angolo.

    tan α = \( \frac{sen \alpha }{cos \alpha } \)


    Funzioni trigonometriche e triangoli rettangoli

    Quando si considera un triangolo rettangolo generico valgono le seguenti relazioni:

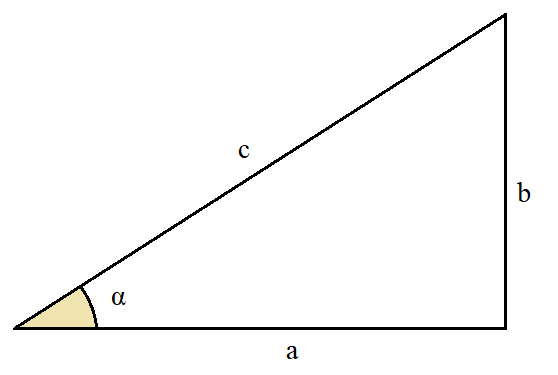
    triangolo rettangolo

    a2 + b2  = c2
    \( c = \sqrt[]{a^2 + b^2} \)  

     e dalla trigonometria anche:

    \( a = c · cos \alpha \)

    \( b = c · sen \alpha \)

    \( tan \alpha = \frac{b}{a} \)


  • Numeri complessi: definizione e rappresentazioni

    E' necessario definire l'unità immaginaria j tale che:

    \( j^2 = -1 \)
     \( j = \sqrt[]{-1} \)

    In tal modo si può definire tutto il campo dei numeri immaginari positivi e negativi fino all'infinito.

    I numeri immaginari possono essere rappresentati, come i numeri reali, su una retta.

    Il piano cartesiano formato sull'asse delle ascisse dai numeri reali R e sull'asse delle ordinate dai numeri immaginari Im è detto piano di Gauss. Un numero complesso si può individuare sul piano di Gauss tramite le sue coordinate complesse. 

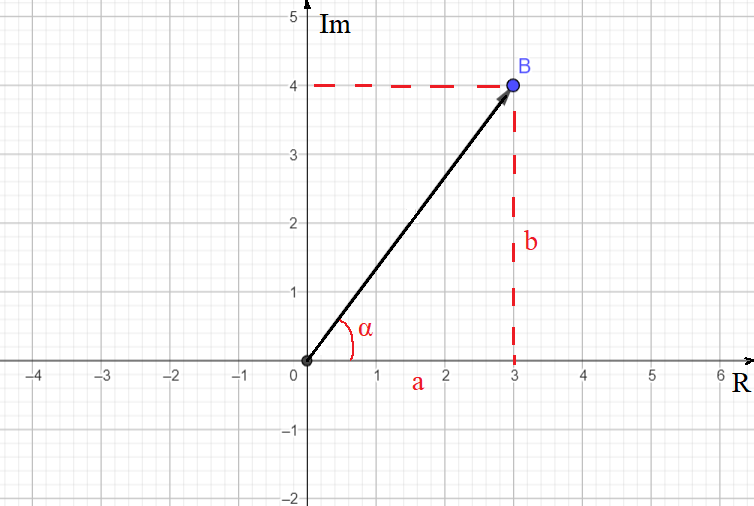
    piano di Gauss

    Un numero complesso si indica con a + jb , dove a è la parte reale e b è la parte immaginaria.

    Il segmento orientato OB rappresenta il numero complesso ed è un vettore complesso. 

    Nell'esempio in figura il numero complesso rappresentato è 3 + j4.

    La lunghezza del vettore OB viene chiamata MODULO, mentre l'angolo α viene chiamato FASE.

    Per quanto visto dalle formule in precedenza, chiamando il vettore ad esempio \( \vec{Z} \) è possibile ricavare la parte reale a e la parte immaginaria b conoscendo modulo e fase e viceversa.

    passaggio algebrica-polare

                                     

    Rappresentazione di numeri complessi

    numeri complessi rappresentazione

  • Operazioni coi numeri complessi

    somma algebrica numeri complessi

    prodotto e rapporto con numeri complessi in forma polare

  • Somma e differenza grafica tra vettori di numeri complessi

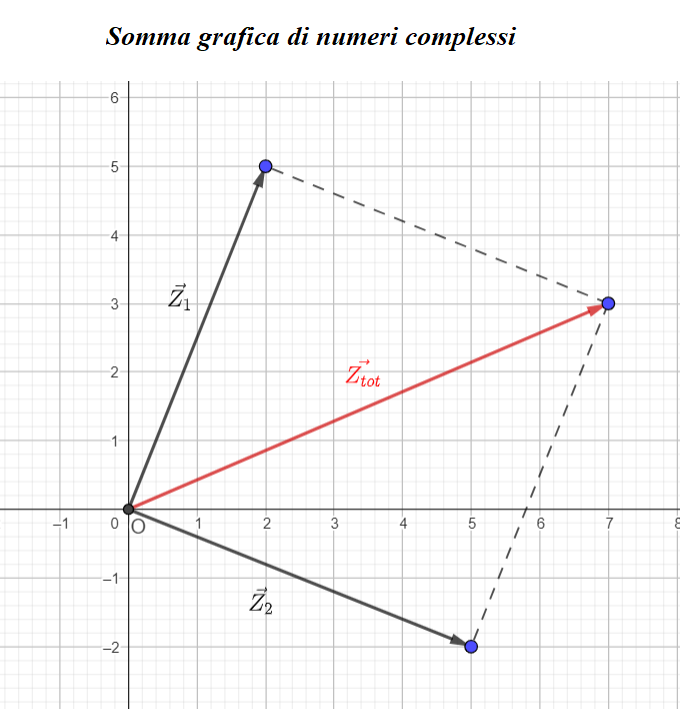
    somma vettori

    \( \vec{Z_{tot}} = \vec{Z_1} + \vec{Z_2} = (2 + j5) + (5 - j2) = 7 + j3 \)

    Per fare la somma di 2 vettori si costruisce il parallelogramma e il vettore somma andrà dall'origine al punto opposto.

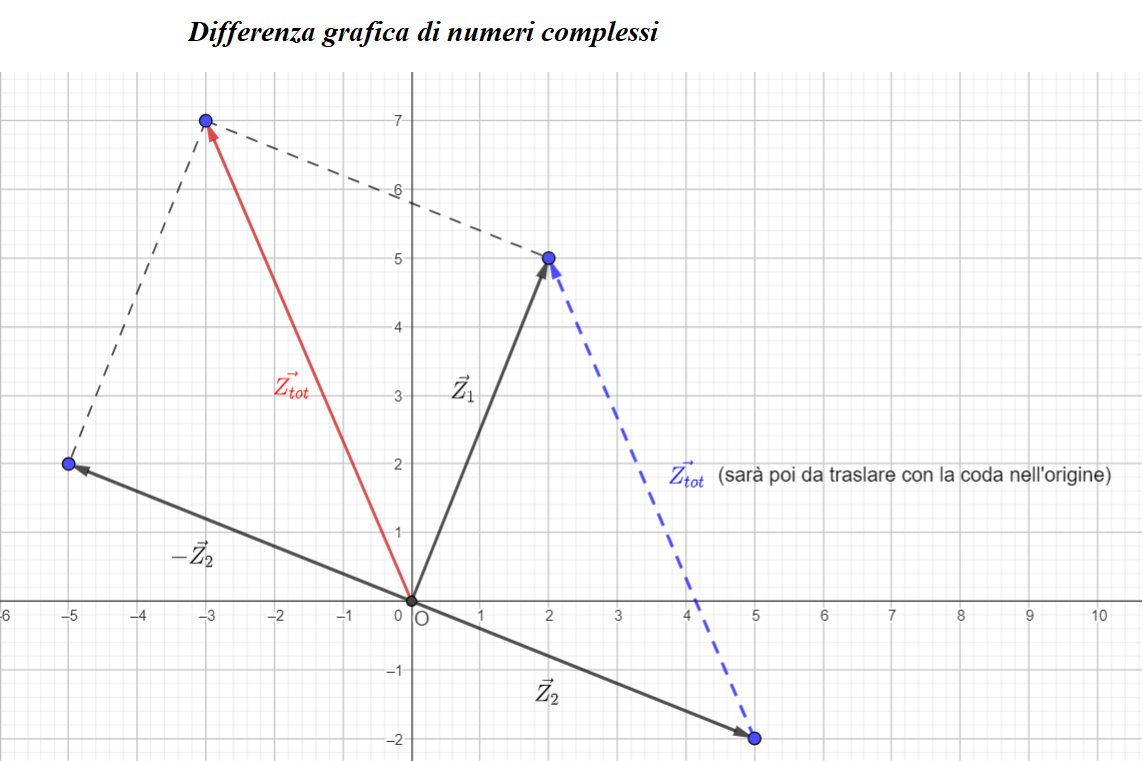
    differenza grafica vettori

    \( \vec{Z_{tot}} = \vec{Z_1} - \vec{Z_2} = (2 + j5) - (5 - j2) = -3 + j7 \)

    Per la differenza tra 2 vettori è possibile fare la somma tra il primo e l'opposto del secondo oppure unire le punte e poi traslare nell'origine.

  • Sfasamento tra numeri complessi

    sfasamento tra numeri complessi 1