Indice degli argomenti
-
Si dicono quadripoli equivalenti quelli che, avendo lo stesso segnale di ingresso, producono lo stesso segnale di uscita pur avendo struttura interna differente.
Se il quadripolo è composto da componenti passivi e si ha un'attenuazione di potenza in uscita si chiama quadripolo passivo; in caso la potenza di uscita sia maggiore di quella in ingresso si ha un quadripolo attivo.
Esistono dei modelli che rappresentano i quadripoli; limitando lo studio a segnali sinusoidali è possibile utilizzare il metodo simbolico.

Modello a parametri Z
Se si scelgono come variabili indipendenti le correnti di ingresso e di uscita, il quadripolo può essere descritto dal seguente sistema di equazioni:
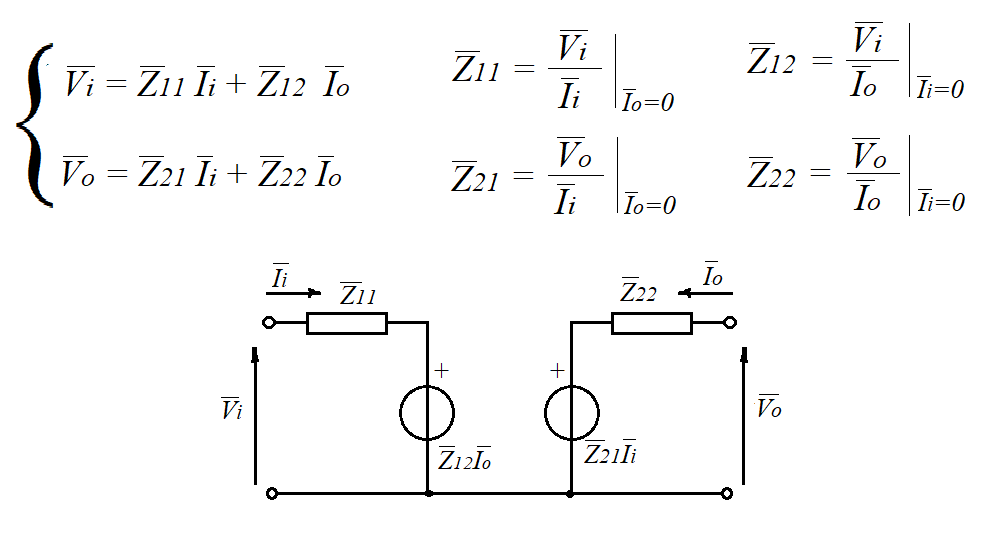
I coefficienti delle correnti sono delle impedenze ottenibili o annullando la corrente in uscita (circuito aperto in uscita) per \( \vec{Z_{11}}\) e \(\vec{Z_{12}}\) oppure annullando la corrente in ingresso per \(\vec{Z_{21}}\) e \(\vec{Z_{22}}\).
Nel caso di quadripoli passivi vale il teorema di reciprocità che rende possibile scambiare ingresso con uscita. Utilizzando tale teorema si ha che \( \vec{Z_{12}}= \vec{Z_{21}} \) e il modello a parametri Z diventa il seguente:
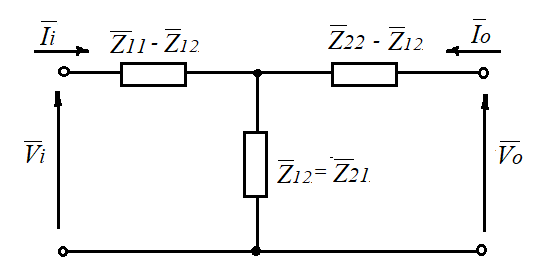
chiamato modello a T.
Modello a parametri Y
Scegliendo come variabili indipendenti le tensioni di ingresso e uscita, , il quadripolo può essere descritto dal seguente sistema di equazioni:
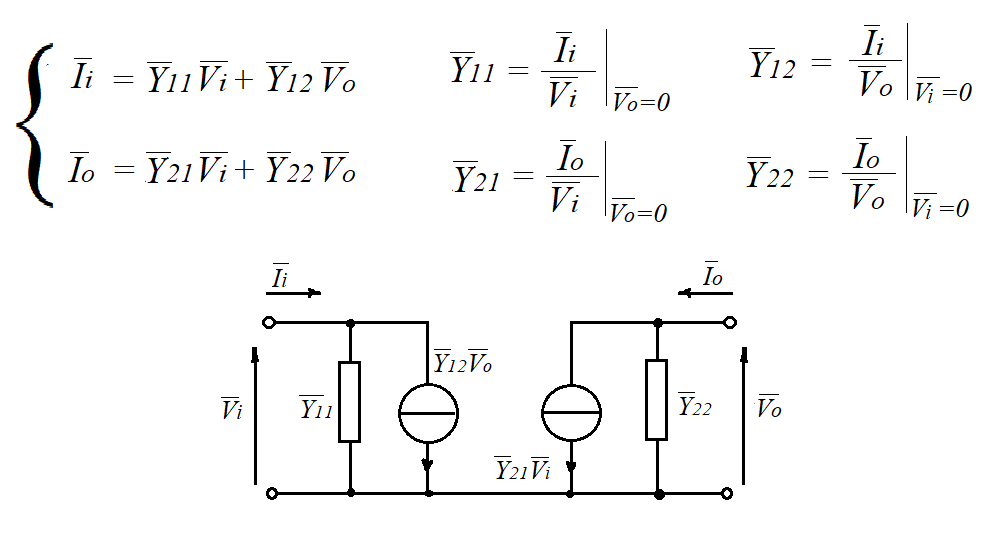
I coefficienti delle tensioni sono delle ammettenze ottenibili o annullando la tensione in uscita (corto circuito in uscita) per \(\vec{Y_{11}}\) e \(\vec{Y_{12}}\) oppure annullando la tensione in ingresso per \(\vec{Y_{21}}\) e \(\vec{Y_{22}}\) (corto circuito in ingresso).
Anche in questo caso, se il quadripolo è reciproco, è possibile ricondurlo ad un modello chiamato modello a π.
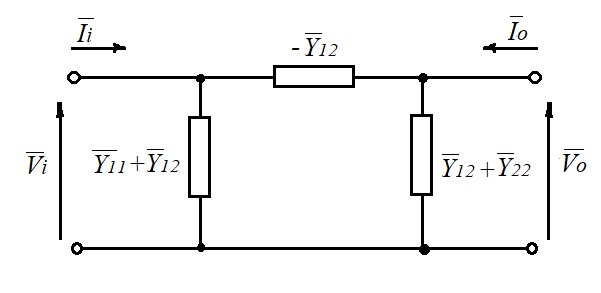
-
Impedenza di ingresso
È il rapporto tra tensione di ingresso Vi e corrente di ingresso Ii andando ad annullare l'effetto dei generatori indipendenti interni e in uscita.
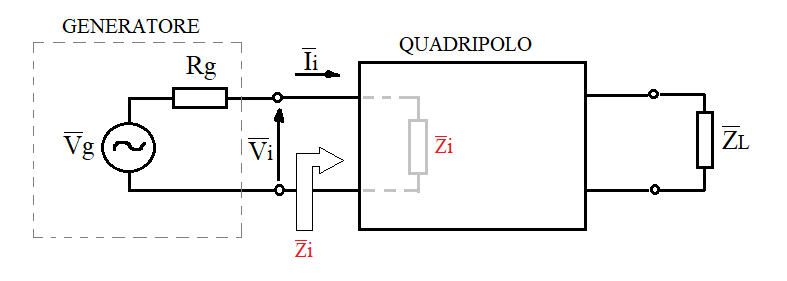
\( \vec{Z_i} = \frac{ \vec {V_i} }{ \vec{I_i} } \)
Se nel quadripolo o nel carico ci sono elementi reattivi allora l'impedenza di ingresso ha una componente immaginaria che dipende dalla frequenza del segnale sinusoidale di ingresso.
Impedenza di uscita
È l'impedenza vista ai morsetti di uscita andando ad annullare l'effetto dei generatori indipendenti interni e in ingresso (esattamente come nel Teorema di Thevenin).
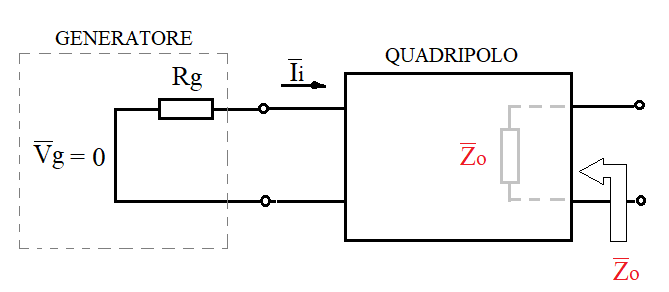
\( \vec{Z_o} = Z_{th} \)
L'impedenza di uscita è influenzata dal valore della resistenza interna del generatore di ingresso Rg .
Se nel quadripolo ci sono elementi reattivi allora l'impedenza di uscita ha una componente immaginaria che dipende dalla frequenza del segnale sinusoidale di ingresso.
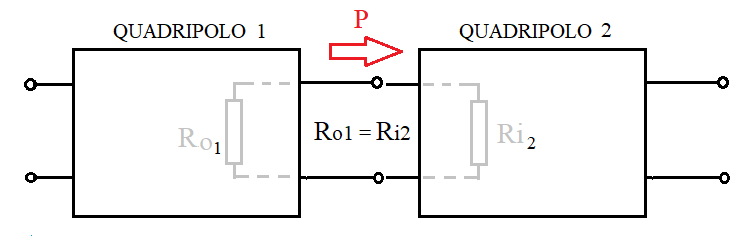
Conoscere le impedenze di ingresso e di uscita è fondamentale per poter studiare ed analizzare quadripoli in cascata.
-
L'adattamento in tensione e in potenza consiste nello scegliere in modo opportuno i valori di impedenza in gioco, al fine di massimizzare la tensione o la potenza in ingresso.
Anche in questo caso conoscere il comportamento è fondamentale per studiare quadripoli in cascata, poiché l'uscita del quadripolo a monte non è altro che l'ingresso del quadripolo a valle.
Si pensi ad un semplice circuito in cui si ha un generatore di tensione (con la sua resistenza interna) collegato all'ingresso di un quadripolo avente resistenza di ingresso puramente resistiva. Il generatore può, a tutti gli effetti, rappresentare il circuito equivalente di Thevenin di un altro quadripolo a monte, in cui la sua resistenza interna non è altro che la sua resistenza di uscita (resistenza equivalente di Thevenin).
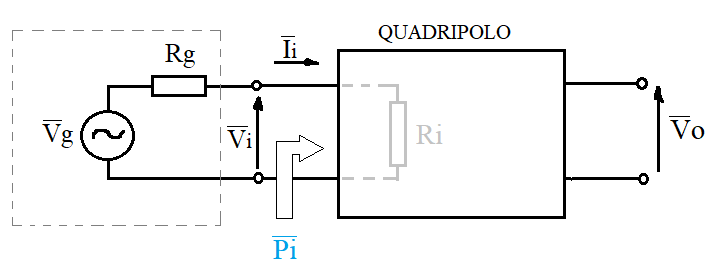
La Vi non è altro che la partizione della Vg .
\( Vi = Vg \cdot \frac{R_i}{R_g + R_i} \)
il suo valore raggiunge il massimo quando \( R_g \ll R_i \); idealmente con \( R_g \rightarrow0 \) e \( R_i \rightarrow \) ∞ (adattamento in tensione).
- \( R_g \) resistenza di uscita dello stadio a monte
- \( R_i \) resistenza di ingresso del quadripolo
Per trasferire la massima potenza da generatore al quadripolo è necessario che:
\( R_i = R_g \)
In tali condizioni (Ri = Rg = R) la potenza vale:
\( P_i = V_i \cdot I_i = \frac{V_g^2}{4R} \)
Nel caso in cui le impedenze non siano puramente resistive, invece, si deve avere:
\( R_i = R_o \) e \( X_i = - X_o \)
Dove vengono realizzati questi adattamenti?- l'adattamento in tensione negli stadi di pre-amplificazione (piccole tensioni) per consentire di collegare quadripoli in cascata senza perdere tensione
- l'adattamento in potenza negli stadi finali di potenza al fine di ottenere il massimo rendimento
-
Come è possibile collegare in cascata due quadripoli se le impedenze di ingresso e di uscita non soddisfano i requisiti richiesti?
Si interpone un circuito chiamato ADATTATORE DI IMPEDENZA:
- adattatori di impedenza per la tensione sono componenti attivi (transistor o amplificatori operazionali che hanno resistenza di ingresso elevata e resistenza di uscita bassa)
- adattatori di impedenza per la potenza sono in genere i trasformatori o anche quadripoli resistivi (che però causano perdite di potenza).
Adattamento di impedenza per la potenza con trasformatore
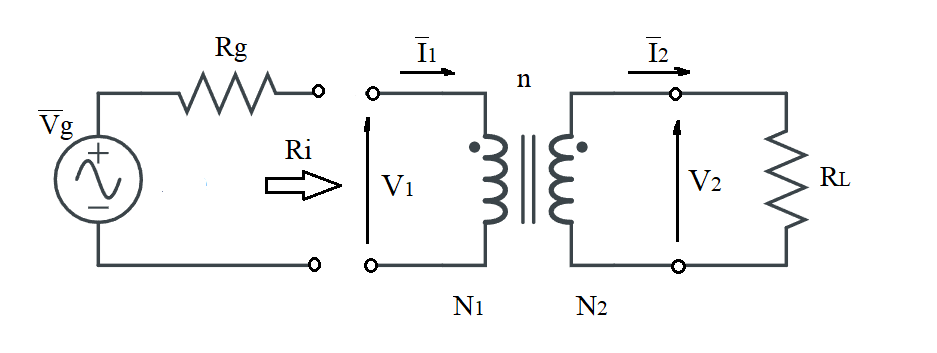
In caso di utilizzo del trasformatore, l'impedenza vista al primario vale
\( R_i = n^2 \cdot R_L \)
quindi per adattare un generatore con resistenza interna Rg al carico RL basta dimensionare opportunamente il rapporto di trasformazione n.
\( n = \frac{N_1}{N_2} = \frac{V_1}{V_2} = \sqrt[]{ \frac{R_g}{R_L}} \)
-
Le IMPEDENZE IMMAGINE di un quadripolo sono due valori \( \vec{Z_{im1}} \) e \( \vec{Z_{im2}} \) tali che:
- se si collega in ingresso l'impedenza \( \vec{Z_{im1}} \) allora l'impedenza di uscita vale \( \vec{Z_{im2}} \)
- se si collega in uscita l'impedenza \( \vec{Z_{im2}} \) allora l'impedenza di ingresso vale \( \vec{Z_{im1}} \)
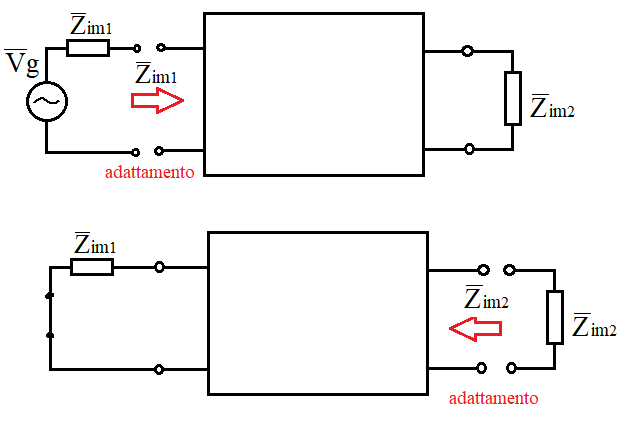
Se si vuole realizzare un adattamento in potenza sia in ingresso che in uscita al quadripolo è necessario collegare a monte un circuito con un'impedenza di uscita pari a \( \vec{Z_{im1}} \), mentre a valle un circuito con impedenza di ingresso pari a \( \vec{Z_{im2}} \).
Il nome "impedenza immagine" deriva proprio dal fatto che ogni circuito "vede" all'altro capo la sua immagine.
Come si calcolano i valori delle impedenze immagine?
\( \vec{Z_{im1}} = \sqrt[]{ \vec{Z{ia} \cdot } \vec{Z{ic}} } \)
\( \vec{Z_{im2}} = \sqrt[]{ \vec{Z{oa} \cdot } \vec{Z{oc}} } \)
dove:- \( \vec{Z_{ia}} \) è l'impedenza di ingresso con uscita aperta
- \( \vec{Z_{ic}}\) è l'impedenza di ingresso con uscita in cortocircuito
- \( \vec{Z_{oa}}\) è l'impedenza di uscita con ingresso aperto
- \( \vec{Z_{oc}}\) è l'impedenza di uscita con ingresso in cortocircuito
Se un quadripolo è SIMMETRICO le impedenze immagine hanno lo stesso valore e vengono chiamate IMPEDENZA CARATTERISTICA \( \vec{Z_o} \).
\( \vec{Z_o} = \vec{Z_{im1}} = \vec{Z_{im2}} = \sqrt[]{ \vec{Z_a} \cdot \vec{Z_c} } \)
-
I quadripoli possono essere:
- passivi se internamente sono costituiti da componenti passivi (resistori, condensatori, induttori, diodi, ecc)
- attivi se internamente sono costituiti da componenti attivi (transistor o amplificatori operazionali)
Nel caso di quadripoli passivi, il segnale fornito al carico risulta attenuato, poiché una parte di potenza viene dissipata internamente.
Nel caso di quadripoli attivi, il segnale fornito al carico risulta amplificato e la potenza sul carico è maggiore di quella in ingresso (la potenza "aggiuntiva" viene prelevata dall'alimentazione in continua).
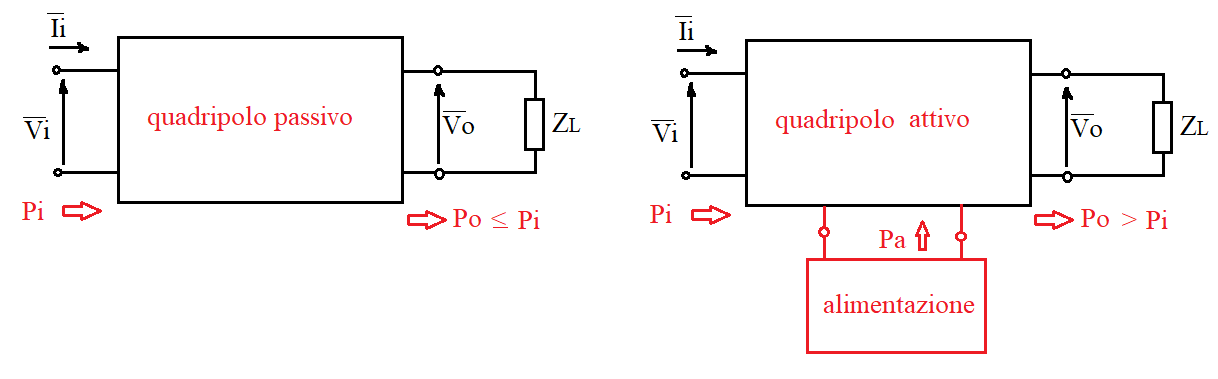
Si possono definire, ad una certa frequenza, i parametri caratteristici:
- GUADAGNO DI TENSIONE è il rapporto tra la tensione di uscita e quella di ingresso (rapporto di ampiezze)
\( G_v = \frac{V_o}{V_i} \)
- GUADAGNO DI CORRENTE è il rapporto tra la corrente in uscita e quella in ingresso
\( G_i = \frac{I_o}{I_i} \)
- GUADAGNO DI POTENZA è il rapporto tra la potenza in uscita e quella in ingresso
\( G_p = \frac{P_o}{P_i} \)
Nei quadripoli passivi il guadagno è < 1 mentre in quelli attivi è ≥ 1.
Se il quadripolo contiene elementi reattivi(C e L) allora il guadagno avrà una parte reale ed una immaginaria, quindi si considera il modulo.
Il guadagno viene generalmente espresso in decibel (dB) definito come:
GUADAGNO DI POTENZA IN dB : \( G_{p|db} = 10 Log (G_p) \)
GUADAGNO DI TENSIONE IN dB : \( G_{v|db} = 20 Log (G_v) \)
Il vantaggio di utilizzare i decibel sta nello sfruttare le proprietà dei logaritmi che permettono di sommare anziché moltiplicare.
Un valore negativi in dB esprime un guadagno < 1 (attenuazione), mentre un valore positivo in dB esprime un guadagno > 1 (guadagno in senso letterale). Il guadagno unitario corrisponde a 0 dB. -
La risposta di un quadripolo è l'andamento nel tempo del segnale di uscita vo(t) quando all'ingresso del quadripolo viene posto un dato segnale vi(t) detto eccitazione.
Occuparsi dell'analisi dei segnali è importante per definire modelli matematici che permettano di prevedere la risposta di un quadripolo ad un segnale qualunque in ingresso.
La funzione di trasferimento
La funzione di trasferimento (fdt) è il rapporto G(s) tra le trasformate di Laplace del segnale di uscita Vo(s) e del segnale di ingresso Vi(s).
\( G(s) = \frac{V_o(s)}{V_i(s)} \)
Conoscendo la fdt di un quadripolo è possibile calcolare la risposta ad un segnale di ingresso qualsiasi.
\( V_o(s) = G(s) \cdot V_i(s) \)
facendo poi l'antitrasformata di Laplace, si risale alla risposta nel tempo.
\( v_o(t) = L^{-1 } [V_o(s)] \)
-
-
